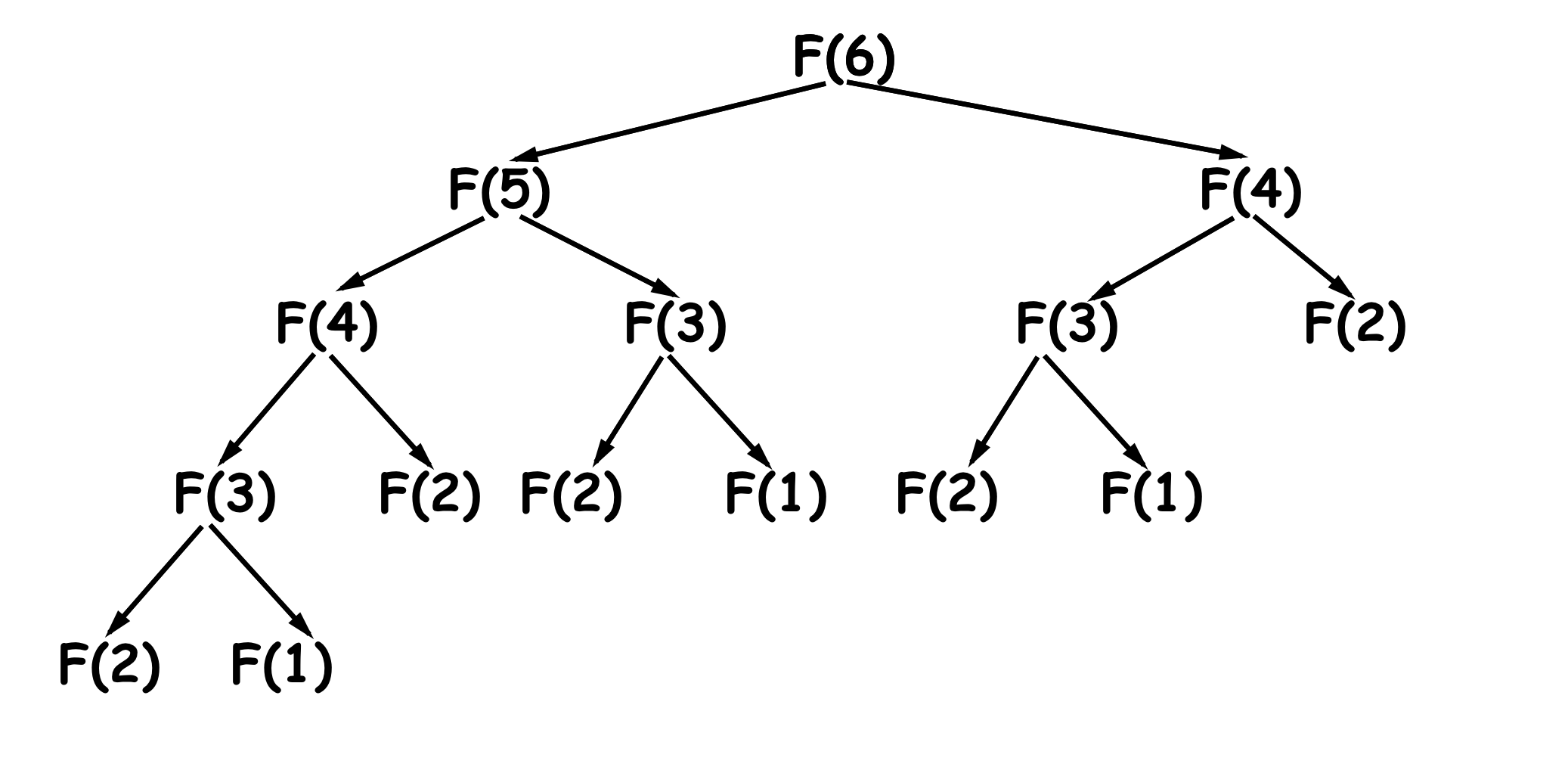
Table of Contents

1. The Challenge
2. Initial recon
3. Algorithm Optimization
   1. Dynamic programming (the Bottom-up approach)
   2. Memoization (Top-down approach)
4. Solution
   1. Allocating memory for our memoization code, and for our results array
   2. How we will add code at the beginning and end of recursive_fun
   3. First shellcode: checking if the result is already computed at the beginning of the function
   4. Second shellcode: cache results at the end of the function
   5. How to assemble shellcodes
   6. Other things to keep in mind
   7. Final gdb script that automates solving it (using the peda patch command)

The Challenge

We are given a binary file, and a short challenge description, you can download the file here

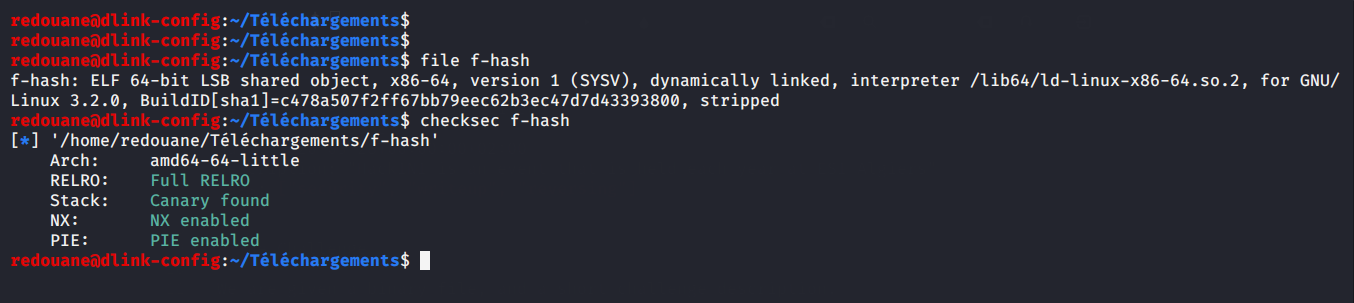
The given file is a 64bit ELF executable.

Initial recon

as the challenge description states that the binary is not working, we expect it to have corrupt headers, or to segfault because of a programming error.

We run it, and nothing happends, it just keeps running

Let’s do a first check with a reverse-engineering framework, let’s check with Ghidra. (note: this is a quick solution, how I solved it with a minimum effort, and no, I did not reverse-engineer all of it).

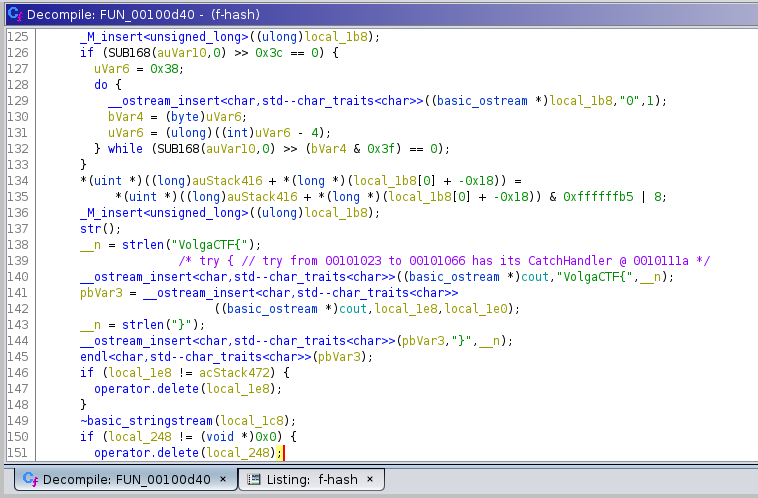
Just by looking at the pseudocode of the main function, generated by Ghidra, we can tell that this was probably written in C++, and that it should print VolgaCTF{...} (you can see how line 140 looks like std::cout, and should print to stdout).

The program is probably stuck before reaching this point, in order to find out, we will run it with a debugger, interrupt its execution (hitting CTRL+C), get which part of the code it’s executing, and try to find out why it’s stuck.

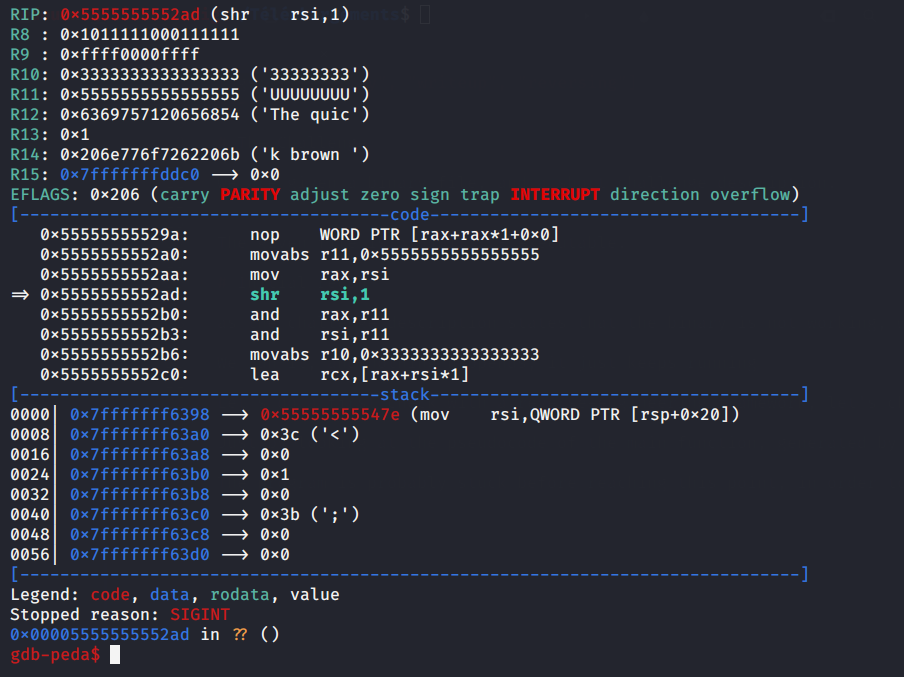
Since the program is compiled with PiE enabled (ie: it’s position-independent), we must substract the address from where the binary is loaded in memory (found in /proc/<pid>/maps, or viewable via the vmmap peda command), to get the offset to one address inside the region of code where the program is stuck, we find the offset 0x12ad.

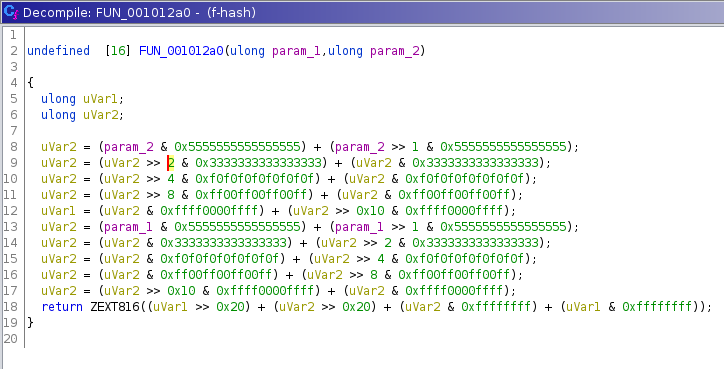
Nothing that could loop forever here, it looks like a cryptographic function, we will name it PRF_1 (for Pseudo Random Function), let’s find XREFS to this function (where it is called from).

It’s called in 3 places, from the same function, let’s check that function.

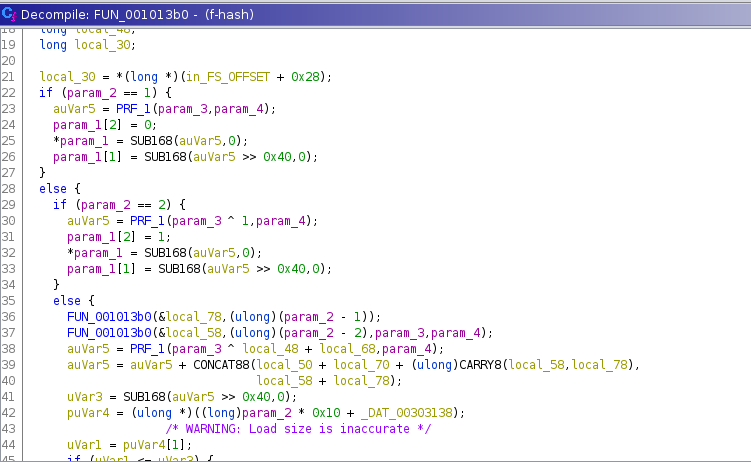
We already see something odd, inside the else statement, the function FUN_001013b0 calls itself, once with param_2 - 1 and once with param_2 - 2, maybe it’s an unoptimized recursive call that is taking forever to finish?

Let’s call FUN_001013b0 recursive_fun, and find out where it’s called from (using XREFS)

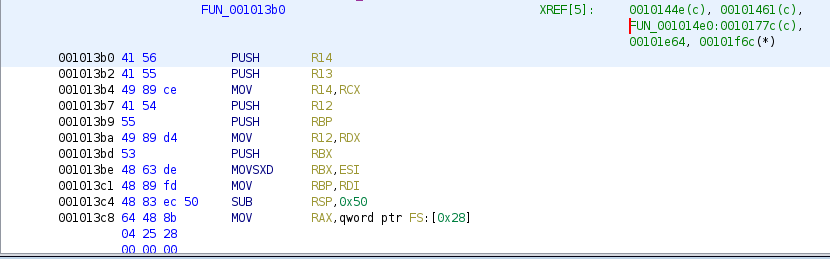
Ignore the first two calls, they are the recursive ones, it’s only called from FUN_001014e0.

Let’s put a breakpoint here, check if it gets hit (or if the binary hangs before reaching it), if it’s hit, we will step over, and check if this function is the culpit. b *0x0000555555554000+0x177c

(note: the base address of the binary should change randomly on each run (because of PiE), but gdb disables randomization by default, disable-randomization is ON)

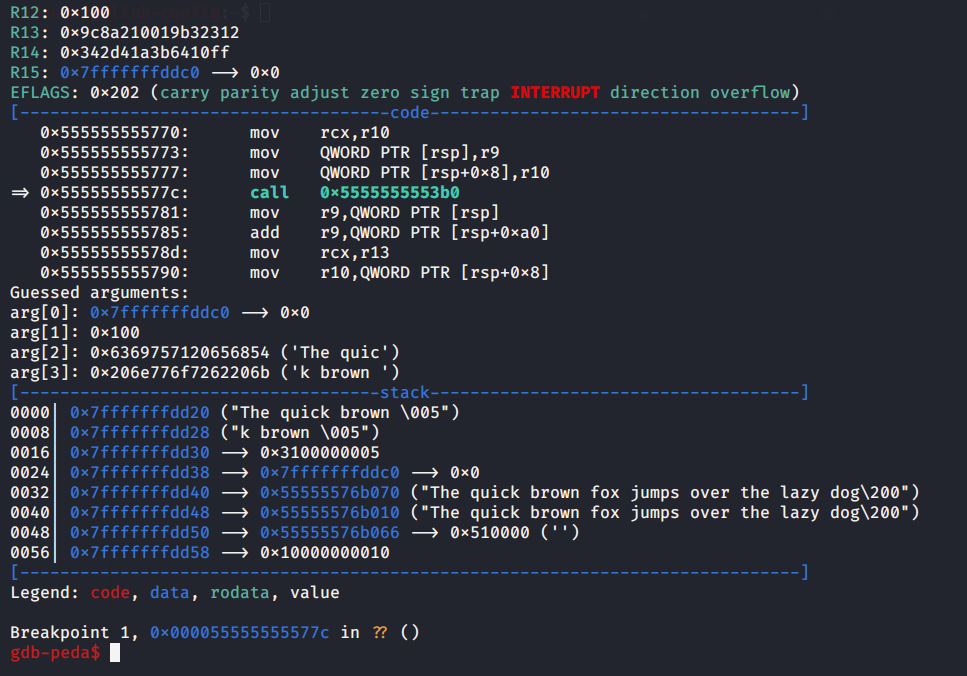
The breakpoint is hit, and we see the arguments passed to the function:

Guessed arguments:
arg[0]: 0x7fffffffddc0 --> 0x0 
arg[1]: 0x100 
arg[2]: 0x6369757120656854 ('The quic')
arg[3]: 0x206e776f7262206b ('k brown ')

When we enter nexti to step over the call, the program doesn’t respond, this means, this function is probably where it’s stuck.

Let’s check recursive_fun more carefully. the second argument looks like an integer, let’s name it i, third and fourth ones look like unsigned long longs, let’s name them x and y, and the first one looks like a buffer, let’s name it buf.

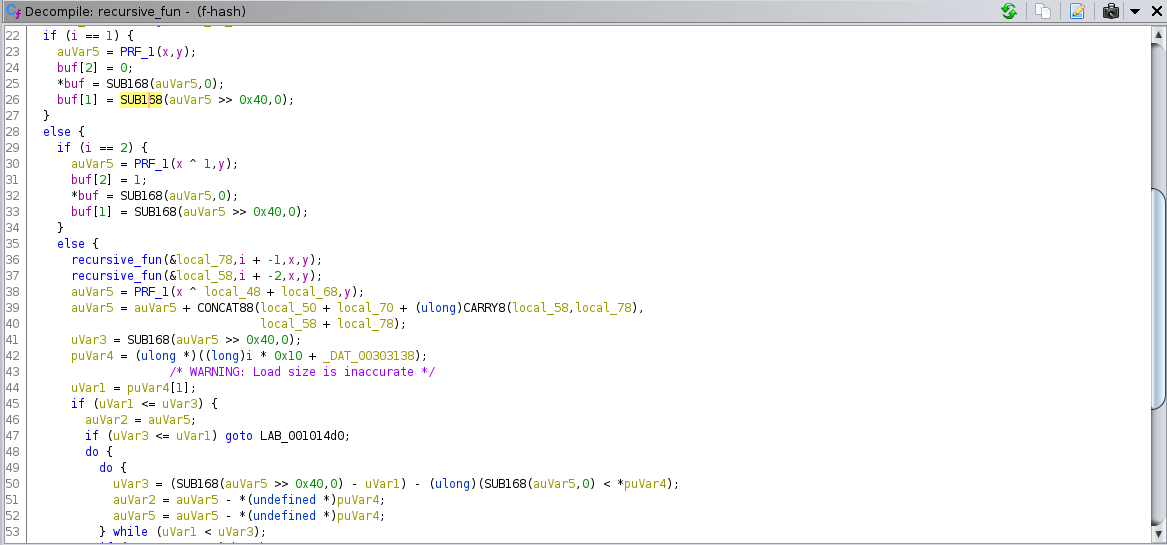
This gives a high-level view of the function, not all of this pseudocode is accurate through, but we can already see that the function behaves like this (in pseudocode):

unsigned long long* recursive_fun(unsigned long long* buf, int i, unsigned long long x, unsigned long long y)
{
	if i == 1
		rdx:rax = PRF_1(x,y)
		buf[0] = rax; buf[1] = rdx; buf[2] = 0;
	else if i == 2
		rdx:rax = PRF_1(x,y)
		buf[0] = rax; buf[1] = rdx; buf[2] = 1;
	else
		unsigned long long a[3];
		unsigned long long b[3];
		recursive_fun(a, i-1, x, y)
		recursive_fun(b, i-2, x, y)
		rdx:rax = PRF_1(x ^ b[3] + a[3], y)
		
		< RUN OTHER CODE >
		
		buf[0] = rax; buf[1] = rdx; buf[2] = r13;
	end
}

The missing code reads data from a global array, and does some computations based on what the call to PRF_1, the global array data, and what the recursive calls returned.

Algorithm Optimization

The question is : how can we compute recursive_fun efficiently?

We see that in recursive calls, only the value of i changes, the function looks like a (complicated) variant of the fibonacci function, we have a recurrent relation of the form:

recursive_fun(1) = const_A
recursive_fun(2) = const_B
recursive_fun(i) = f(recursive_fun(i-1), recursive_fun(i-2))

for fixed x,y values, some constants const_A, const_B, and a function f that can be computed in polynomial time.

The inefficience of this implementation stems from the fact that the function has overlapping subproblems, and the recursive implementation wastes time recomputing them again and again, consider for example, a call to recursive_fun with i=6

to compute recursive_fun(6), it’s necessary to compute recursive_fun(5) once, recursive_fun(4) twice, recursive_fun(3) three times, recursive_fun(2) 5 times, and recursive_fun(1) three times, as the value of i gets larger, we get a combinatorial explosion, the number of computations quickly gets out of hands. To efficiently compute values of recursive_fun, we have two possible solutions:

Dynamic programming (the Bottom-up approach)

Maintain an array dp where dp[i] = recursive_fun(i), initially empty.

dp[1] = recursive_fun(1)
dp[2] = recursive_fun(2)
for i from 3 to 0x100
	dp[i] = f(dp[i-1], dp[i-2])
done

at the end, computing values of recursive_fun becomes as trivial as reading from the array.

Memoization (Top-down approach)

maintain an array results, initially empty.

Modify the function recursive_fun:

typedef unsigned long long ull;
unsigned long long* recursive_fun(ull* buffer, int i, ull x, ull y)
{
	if (results[i] is set)
		copy results[i] to buffer // already computed, just return it
	else
		< CODE FROM THE ORIGINAL recursive_fun, THAT COMPUTES THE RESULT IN buffer >
		copy buffer to results[i]; // store it, so that future calls with the same i will return the cached one
	end
}

It’s efficient because the solution of each subproblem is computed once, and stored, subsequent calls will read it from the array (and thus preventing the creation of a larger call tree).

Solution

The solution most people will think of, is to reimplement the function using one of the techniques above, in a separate program, and get what it should return, at first, that’s what I was doing, but then, I got a better idea (and more guaranteed to work without hard-to-debug problems), what if I added memoization code to the already-compiled function? it’s just code added at the beginning (to check if it was already computed), and at the end (to cache the result).

The advantages of doing this is:

• I don’t need to know exactly how recursive_fun works, how the f function works exactly.
• It is more guaranteed to work from the first time, without debugging.

So, let’s start :D

Allocating memory for our memoization code, and for our results array

We will do everything inside a gdb debugging session, as it disables randomization, and supports scripting.

First, we allocate 1024 bytes for our memoization code, we make the allocation at a fixed address (0x10000), and with executable protections (as it’s for our injected code).

set $cave1 = mmap(0x10000, 0x400, 7, 0x32, -1, 0)

for the results array, since recursive_fun returns three unsigned long longs, each element of it will contain 4 fields : the first three are as returned by recursive_fun, the fourth one, when 1 marks the element as existent, when 0 marks it as free. That is 32 bytes for each entry of it, we will allocate it with:

set $results = mmap(0x20000, 0x101*32, 3, 0x32, -1, 0)

(0x101 elements, so that $results[0x100] is bound, and is what the function computes). Since we need two codecaves: one for the memoization code running at the beginning of the function, and one at the end, we will set:

set $cave2 = $cave1+0x200

0x200 bytes is largely enough.

How we will add code at the beginning and end of recursive_fun

In order to insert code at a certain line in the function, we will:

1. overwrite that line with a jmp to our code (and nops if necessary, to keep code valid)
2. at the end of our code, run the original code that was at that line, and was overwritten
3. jmp back to where we left, right after the overwritten bytes

We will number each shellcode, as well as the address where it will be written.

Since our $cave1 is at 0x10000, we will patch the beginning of recursive_fun:

1. at address 0x5555555553b0 with:

mov rax,0x10000
jmp rax

this takes 7 bytes, and overwrites the instructions

push r14
push r13
mov r14, rcx

So we need to run them at the end of our code at $cave1 (if we are returning to execute the function, otherwise, if the result is cached, we can return straight away from the function).

First shellcode: checking if the result is already computed at the beginning of the function

	if results[i][3] == 1
		buf[0] = results[i][0]
		buf[1] = results[i][1]
		buf[2] = results[i][2]
		return;
	else
		< GET BACK TO THE FUNCTION, AND LET IT COMPUTE THE SOLUTION >
	end

So, if the result is already computed, it will not even execute the code inside recursive_fun.

2. code in $cave1:

mov rax,0x20000 ; address of results
push rsi
shl rsi, 5
add rax,rsi     ; rax = &results[i]
cmp byte[rax+24],1 ; check if the 4rd field is 1
je cached
pop rsi       ; not in the array, just do what was going to be done at the beginning of the function, and continue from there
push r14
push r13
mov r14, rcx
mov rax, 0x5555555553b7
jmp rax
cached:
mov rsi, [rax]    ; already computed, copy the computed values in buf, and return
mov [rdi], rsi
mov rsi, [rax+8]
mov [rdi+8], rsi
mov rsi, [rax+16]
mov [rdi+16], rsi
pop rsi
ret

shl rsi, 5 multiplies i by 32 (size of an element of results), and 0x20000+i*32 is the address where the array element should be.

Second shellcode: cache results at the end of the function

	results[i][0] = buf[0]
	results[i][1] = buf[1]
	results[i][2] = buf[2]
	results[i][3] = 1

The problem we find when trying to do it in assembly is that we don’t find a way to access i at the end of the function, remember, it was a function argument, passed in the rsi register, and copied into rbx, but both had their values changed inside the function (and maybe recursive calls), so, how do we get it?

We can’t make the shellcode in $cave1 store it in a register, otherwise, recursive calls would change it, it needs to be stored in the storage of the function executing (one if its local variables for example), but one that is never changed.

For this, I got a pretty clever idea, as the index needs to be saved in the stackframe of the function (as one if its local variables that is never changed inside the function for example), so that recursive calls don’t change it, and I noticed the function is protected with a stack canary, why not save the index instead of the canary? :p

The stack smashing protector (also called stack canary) is a random value that is saved on the stack at the beginning of the function, and checked for changes when the function is about to return, to detect buffer overflows, we are pretty sure that no code will change it after it’s set.

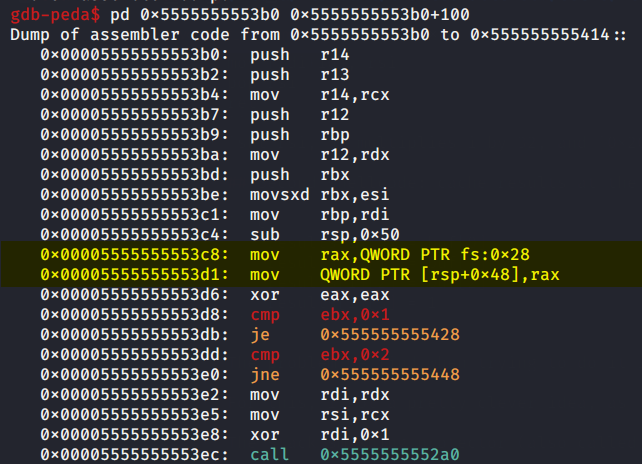
3. The canary is saved at [rsp+0x48], we will just replace mov [rsp+0x48], rax at address 0x5555555553d1 with :

mov [rsp+0x48], rsi

at that instruction to make it store i instead.

The end of the function (where it returns) looks like this: it checks if the canary has changed, if yes, probably calls __stack_chk_fail or abort, otherwise, cleans the stack and returns.

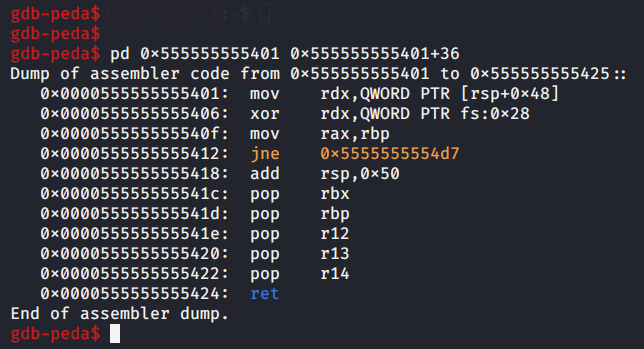
after the first instruction, i will be in rdx, So, for our shellcode, we will use rdx as an index.

4. at $cave2:

mov rax, 0x20000
shl rdx, 5
add rax, rdx
mov rdx, [rbp]
mov [rax], rdx
mov rdx, [rbp+8]
mov [rax+8], rdx
mov rdx, [rbp+16]
mov [rax+16], rdx
mov byte[rax+24], 1
mov rax, rbp
add rsp, 0x50
pop rbx
pop rbp
pop r12
pop r13
pop r14
ret

Note: I added the code at the end of the function in $cave2, in order to return directly from there to the caller of recursive_fun.

Finally, the jmp to $cave2 should be done right after the stack canary is read (at the end of the function, to cache the result, rbp = buf in this case).

5. At 0x0000555555555406

mov rax, 0x10200
jmp rax
db 0x90,0x90

0x10200 is the address of $cave2, I added 2 nop instructions to keep my patch to the size of an instruction, but since I am not returning from $cave2, that’s optional.

Everything is ready.

How to assemble shellcodes

It’s very simple to assemble shellcodes, using rasm2, like:

cat |rasm2 -ax86.nasm -b64 -f- <<EOF
mov rax, 0x10000
jmp rax
EOF

Other things to keep in mind

It turns out that recursive_fun is called multiple times from the same address with different x and y values, and i = 0x100, it’s necessary to clear the results array between two successive calls, otherwise, it will be using previously cached values that are wrong. We will clear it with

p (void*)memset($results, 0, 0x101*32)

Final gdb script that automates solving it (using the peda patch command)

I’ve numbered each shellcode, as well as the address where it should be (see on the top). The patch command writes the results of assembing the shellcodes (returned by nasm, which is used by rasm2), into the target addresses.

In total, recursive_fun is called five times.

b *0x000055555555577c
r
set $cave1 = mmap(0x10000, 0x400, 7, 0x32, -1, 0)
set $cave2 = $cave1 + 0x200
set $results = mmap(0x20000, 0x101*32, 3, 0x32, -1, 0)

printf "cave1 at %p\ncave2 at %p\nresults at %p\n", $cave1, $cave2, $results
patch 0x5555555553b0 "\xb8\x00\x00\x01\x00\xff\xe0"
patch 0x0000555555555406 "\xb8\x00\x02\x01\x00\xff\xe0\x90\x90"
patch 0x5555555553d1 "\x48\x89\x74\x24\x48"
patch $cave1 "\xb8\x00\x00\x02\x00\x56\x48\xc1\xe6\x05\x48\x01\xf0\x80\x78\x18\x01\x0f\x84\x14\x00\x00\x00\x5e\x41\x56\x41\x55\x49\x89\xce\x48\xb8\xb7\x53\x55\x55\x55\x55\x00\x00\xff\xe0\x48\x8b\x30\x48\x89\x37\x48\x8b\x70\x08\x48\x89\x77\x08\x48\x8b\x70\x10\x48\x89\x77\x10\x5e\xc3"
patch $cave2 "\xb8\x00\x00\x02\x00\x48\xc1\xe2\x05\x48\x01\xd0\x48\x8b\x55\x00\x48\x89\x10\x48\x8b\x55\x08\x48\x89\x50\x08\x48\x8b\x55\x10\x48\x89\x50\x10\xc6\x40\x18\x01\x48\x89\xe8\x48\x83\xc4\x50\x5b\x5d\x41\x5c\x41\x5d\x41\x5e\xc3"

set $i = 0
while $i < 4
	p (int)memset($results, 0, 0x101*32)
	c
	set $i=$i+1
end

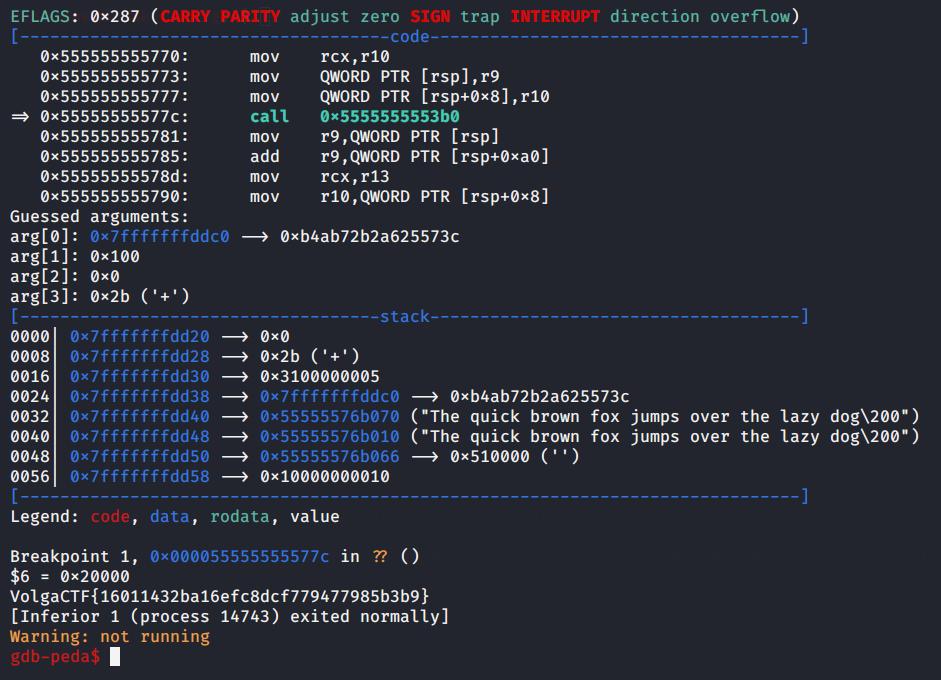
VolgaCTF{16011432ba16efc8dcf779477985b3b9}

Nice challenge.