Inverting Keccak-f if the sponge leaks
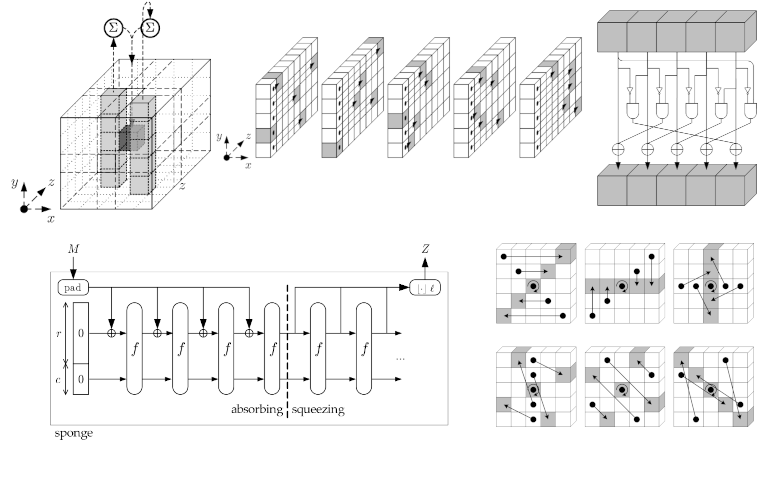
Table of Contents
- What is SHA3
- Why another hash function in the SHA family?
- Deeper view of SHA-3
- Implications
What is SHA3
SHA3 is a family of standarised cryptographic hashing functions, it’s the winner of the 2012 NIST hash function contest.
reminder (click to expand)
a cryptographic hash function is a fast one-way function that associates a fixed-size digest to variable-size inputs, a good hash function must satisfy the following properties:
- Collision resistance: It should be difficult to find two messages that have the same hash.
- Pre-image resistance: given
h, an output of the function, it should be difficult to find a messagemsuch thath = hash(m). - Second pre-image resistance: Given an input
m1, it should be difficult to find another inputm2such thathash(m1) = hash(m2).
Why another hash function in the SHA family?
For over a decade, the most common construction of hash functions was based on block ciphers. Using the so-called Merkle–Damgård construction. Associated with a compression function that is very similar to a block cipher.
All hash functions developed from the 1980s through the 2010s are based on this construction: MD4, MD5, SHA-1, and the SHA-2 family, as well as the lesser-known RIPEMD and Whirlpool functions.
The construction has proven secure enough for most of the properties wanted from a cryptographic hash function, and it’s simple. View it as a way to turn a secure compression function to a secure hash function. However, it has some flaws, for example, it makes hash-length extension attacks possible.
Some of the previously-standarized hash functions have also proven vulnerable, collisions have become practical on some of them (see SHATTERED and MD5 Collisions)
SHA-3 is fundamentally different, it’s not just another similarly-designed hash function with a different compression function. It relies instead on a sponge construction.
Deeper view of SHA-3
The sponge construction
The structure of a sponge construction is illustrated below:
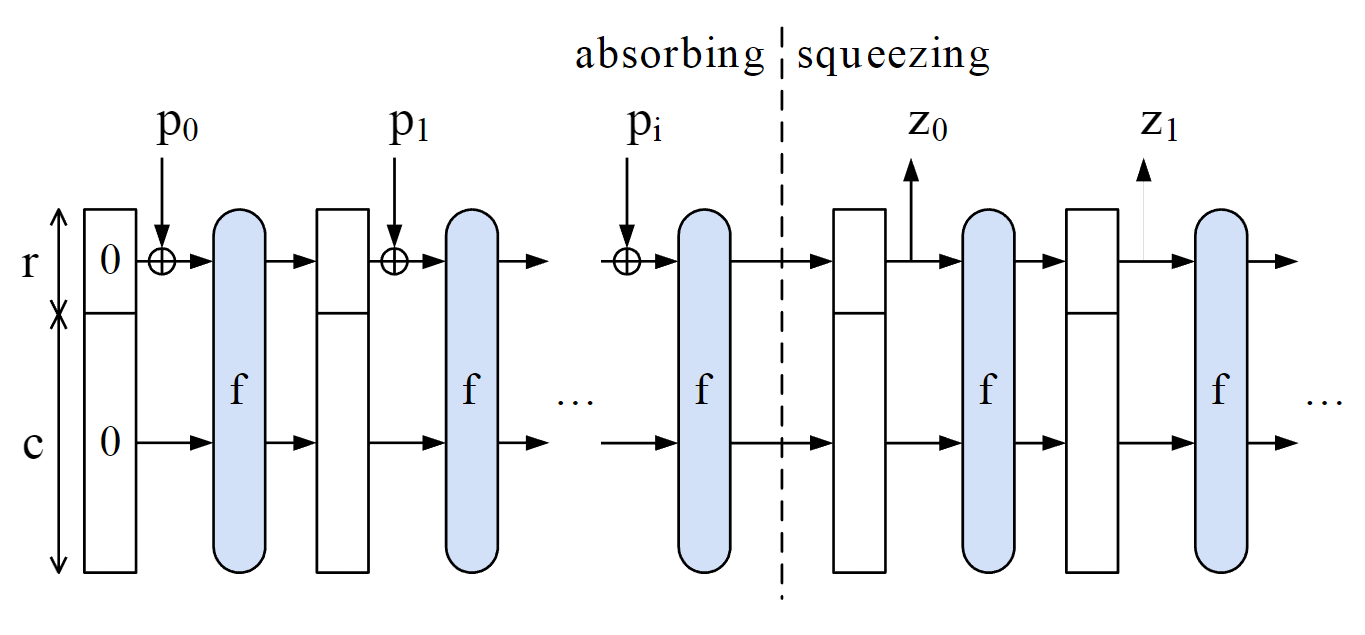
We call the function f the Permutation Function of the sponge construction.
Sponge constructions can be used not only to hash data, but also to generate variable-sized streams of data (which can be used for PRNGs or stream ciphers for example).
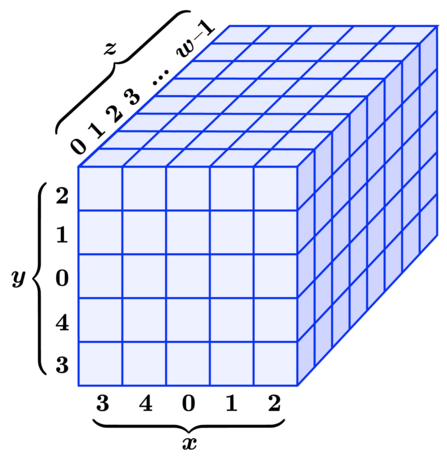
The internal state
The internal state of the hash function has \(r+c\) bits. We represent it as a \(5\times 5\times w\) 3D array of bits, where \(w\) is a power of 2 (\(w = 2^l\)) (in practice, \(w = 64\), so \(r+c = 1600\)).
In the SHA-3 family of hash functions, different functions have different rate and capacity values.
| Function | Capacity \(c\) | Rate \(r\) | Output size \(d\) |
|---|---|---|---|
| SHA3-224 | 448 | 1152 | 224 |
| SHA3-256 | 512 | 1088 | 256 |
| SHA3-384 | 768 | 832 | 384 |
| SHA3-512 | 1024 | 576 | 512 |
The Permutation function at the core of Keccak: Keccak-p
The function at the core of the sponge construction in SHA-3 is called Keccak-p. The steps it consists of are as follow:
Input:
- String
Sof length \( b = 5 \times 5 \times w \) - Number of rounds \( n_r \).
Operations:
- Convert the input string
S(of lengthb) to a 3-dimensional state arrayA(of the shape \( 5 \times 5 \times w \)) . Bits are just rearranged. - Runs the following operations \( n_r \) times (\( i_r \) being the round index, taking the values
0,1, …).- \( A’ = \iota ( \chi ( \pi ( \rho ( \theta ( A ) ) ) ), i_r ) \)
- \( A’ \) becomes the new state
- Convert the state to a string
S(of lengthb), bits are just rearranged, as in the first step.
def keccak_rho(s, nr)
state_from_bitarray s;
l = Math.log(@w, 2).to_i
(12+2*l-nr).upto(12+2*l-1) do|ir|
theta
rho
pi
chi
iota(ir)
end
bitarray_from_state
end
Keccak-f is just Keccak-p with \(12 + 2 \times log_2(w)\) rounds.
def keccak_f(s)
l = Math.log(@w, 2).to_i
keccak_rho(s, 12+2*l)
end
The next subsections will summarize each of these operations.
Theta: \(\theta\)
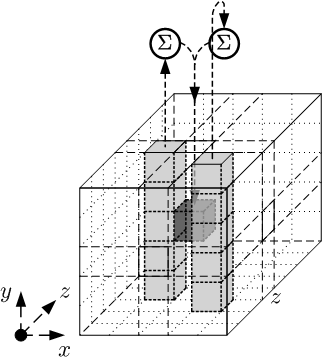
The \(\theta\) operation adds some adjacent columns to each element in the state array. The formal steps are:
- For all pairs \((x, z)\) such that \(0 \leq x < 5\) and \(0 \leq z < w\), let $$C[x, z] = A[x, 0, z] \oplus A[x, 1, z] \oplus A[x, 2, z] \oplus A[x, 3, z] \oplus A[x, 4, z]$$ \(C[x, z]\) is just the sum in \(GF(2)\) of the column at \((x, z)\) (see the screenshot above for an illustration)
- For all pairs \((x, z)\) such that \(0 ≤ x < 5\) and \(0 ≤ z < w\) let $$D[x, z] = C[(x-1)\bmod 5, z] \oplus C[(x+1)\bmod 5, (z-1)\bmod w]$$ \(D[x, z]\) is the sum of the two columns, at \(((x-1)\bmod 5, z)\) and \((x+1)\bmod 5, (z-1)\bmod w\).
- For all triples \((x, y, z)\) such that \(0 \leq x < 5\), \(0 \leq y < 5\), and \(0 \leq z < w\), let $$A’[x, y, z] = A[x, y, z] \oplus D[x, z]$$
Code:
def theta
c = 5.times.map{|x|
@w.times.map{|z|
@state[x][0][z] ^ @state[x][1][z] ^ @state[x][2][z] ^ @state[x][3][z] ^ @state[x][4][z]
}
}
d = 5.times.map{|x|
@w.times.map{|z|
c[ (x-1) % 5 ][z] ^ c[ (x+1) % 5 ][ (z-1) % @w ]
}
}
5.times{|x|
5.times{|y|
@w.times{|z|
@state[x][y][z] ^= d[x][z]
}
}
}
end
Rho: \(\rho\)
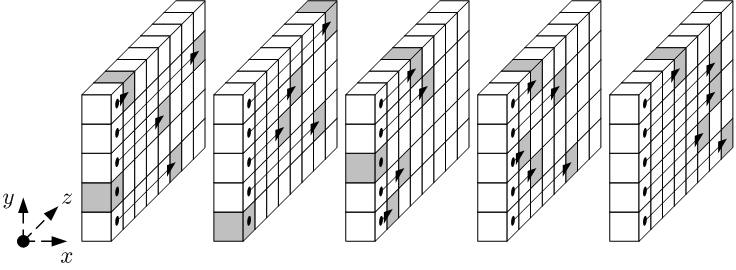
The \(\rho\) operation rotates the bits of each lane by an offset. The steps are:
- For all \(z\) such that \(0 \leq z < w\), let \(A’[0, 0, z] = A[0, 0, z]\).
- Let \((x, y) = (1, 0)\).
- For \(t\) from
0to23:- for all \(z\) such that \(0 \leq z < w\), let \(A’[x, y, z] = A[x, y, (z – (t +1)(t + 2)/2)\bmod w]\)
- let \((x, y) = (y, (2x + 3y)\bmod 5)\).
- \(A’\) becomes the new state.
Code:
def rho
new_state = clone_state # create a clone of the current state
x, y = 1, 0;
0.upto(23) do|t|
@w.times{|z|
new_state[x][y][z] = @state[x][y][( z - ( t + 1 ) * (t + 2) / 2 ) % @w ]
}
x, y = y, (2*x + 3*y) % 5;
end
@state = new_state;
end
Pi: \(\pi\)
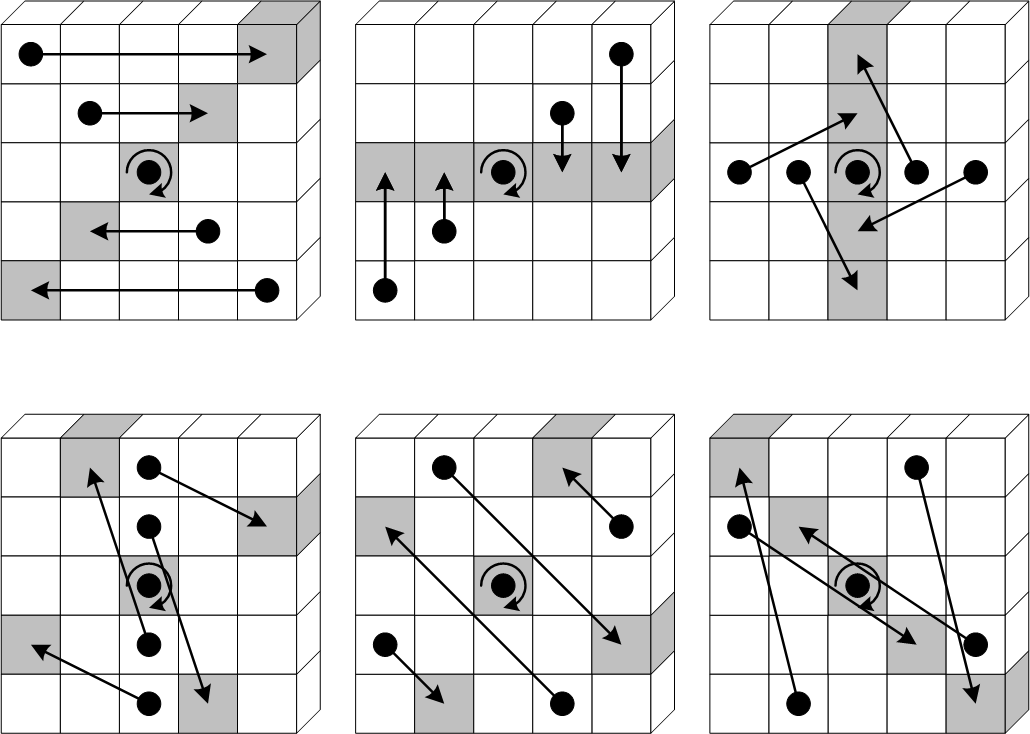
The \(\pi\) operation rearranges the positions of the lanes, also a simple substitution of the bits in the lanes.
- For all triples \((x, y, z)\) such that \(0 \leq x < 5\), \(0 \leq y < 5\), and \(0 \leq z < w\), let \(A’[x, y, z]= A[(x + 3y)\bmod 5, x, z]\).
- \(A’\) becomes the new state.
Code:
def pi
new_state = clone_state
5.times do|x|
5.times do|y|
@w.times do|z|
new_state[x][y][z] = @state[ (x + 3*y) % 5 ][x][z]
end
end
end
@state = new_state
end
Chi: \(\chi\)
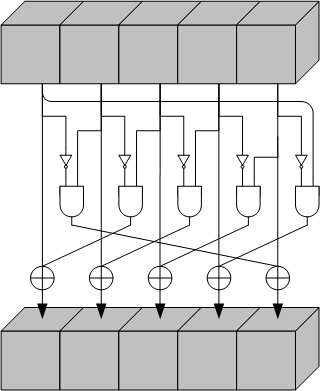
The \(\chi\) operation replaces each bit in the state, with its xor with a non-linear function of two bits from its row.
- For all triples \((x, y, z)\) such that \(0 \leq x < 5\), \(0 \leq y < 5\), and \(0 \leq z < w\), let $$A’[x, y, z] = A[x, y, z] \oplus ((A[(x+1)\bmod 5, y, z] \oplus 1) \wedge A[(x+2)\bmod 5, y, z])$$
- \(A’\) becomes the new state.
Code:
def chi
new_state = clone_state
5.times do|x|
5.times do|y|
@w.times do|z|
new_state[x][y][z] = @state[x][y][z] ^ ((@state[(x+1)%5][y][z]^1) & @state[(x+2)%5][y][z]);
end
end
end
@state = new_state
end
Iota: \(\iota\)
The effect of this operation is to modify some bits of the lane \((0, 0)\) in a manner that depends on the round index \(i_r\).
- Some round constants are calculated, using a simple algorithm that only takes into consideration the round index. \(RC\) is a vector of \(w\) bits. The constant for round \(i_r\).
- Make \(A’\) a copy of \(A\).
- For all \(z\) such that \(0 \leq z <w\), let \(A’[0, 0, z] = A[0, 0, z] ⊕ RC[z]\).
- \(A’\) is the new state.
More details on each of the steps, including the algorithm for calculating round constants, can be found on the original NIST publication.
Code:
def self.rc(t)
#return 1 if t % 255 == 0
r = 1
1.upto(t) do|i|
r <<= 1
r ^= 0x71 if r & 0x100 != 0
#r &= 0xfff
end
r & 1
end
def iota(ir)
rc = [ 0 ] * @w
l = Math.log(@w, 2).to_i
rc = 0
shift = 1
0.upto(l) do|j|
rc |= Keccak.rc(j + 7 * ir) << (shift-1);
shift <<= 1;
end
rc = rc.to_s(2).ljust(64,?0).chars.map(&:to_i)
@w.times do|z|
@state[0][0][z] ^= rc[z];
end
end
Inverting Keccak-p
\(Keccak-p\) is a permutation, as such, it is efficiently invertible. This doesn’t have the disastrous consequences you might think of, the hash function remains safe, and one-way, because the internal state is never returned, and it’s not possible to invert the permutation by having only rate bits of its internal state.
However, this can have some implications if, for example, the whole internal state of the sponge construction gets leaked at some point during the computation.
Inverting \(Keccak-p\) requires inverting each of its steps.
Please note that:
- This is my own attempt at inverting the function, I did not follow any reference to do it, as such, it might not be the most efficient way, but it works.
- The implementation is focused on simplicity and readability, not performance. It’s as close as possible to the specification from the NIST paper.
\( \theta^{-1} \): Back to linear algebra
The \(\theta\) step essentially replaces each element in the state with a sum of 11 elements. For example: $$ A’[2, 2, 4] = A[2, 2, 4] \oplus \\ A[1, 0, 4] \oplus A[1, 1, 4] \oplus A[1, 2, 4] \oplus A[1, 3, 4] \oplus A[1, 4, 4] \oplus \\ A[3, 0, 3] \oplus A[3, 1, 3] \oplus A[3, 2, 3] \oplus A[3, 3, 3] \oplus A[3, 4, 3]$$
My idea to invert this step is to consider \(5\times 5\times w\) equations of \(5\times 5\times w\) unknowns, where unknowns are bits from the state before the application of the \(\theta\) step.
In the matrix form of this system: \(M.B = B’\), where \(B\) is the state before the transformation, \(B’\) after, \(M\) the matrix representing the system.
reminder (click to expand)
Just like the following system: $$ a+c+d = 1\\ a+e+f = 0\\ b+c+d+e+f = 1\\ d+f = 0\\ a+b+e = 1\\ b+d+e+f = 1\\ $$ Can be represented using the following notation: \( M_1.X_1 = X_2 \). Where the matrix \(M\) equals:
\begin{pmatrix} 1 & 0 & 1 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 1 & 1 \\ 0 & 1 & 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 & 0 & 1 \\ 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 1 & 1 \end{pmatrix}
\(X_1\) equals:
\begin{pmatrix} a \\ b \\ c \\ d \\ e \\ f \end{pmatrix}
And \(X_2\): \begin{pmatrix} 1 \\ 0 \\ 1 \\ 0 \\ 1 \\ 1 \end{pmatrix}
If we have \(M^{-1}\), we can efficiently calculate \(B = M^{-1}.B’\), which is the state before the \(\theta\) operation.
for \(w = 64\) (that is, a state matrix having the shape \(5\times 5\times 64\), as in sha3), we would have 1600 equations with 1600 unknowns, where each unknown is a bit.
This involves a lot of calculations, fortunately, we can precompute this inverse matrix, and use it to inverse this step efficiently.
We define a class BinMatrix, which will represent a matrix over the field \(GF(2)\), we implement the Gaussian elimination algorithm for inverting the matrix (check out the final code at the end of the article for implementation details).
# precomputes the inverse of the M matrix we defined above for a given value of w
def precompute_untheta(w)
state_equations = (w*5*5).times.map{|i|
z = i % w
y = (i / w) % 5
x = (i / w / 5)
r = [ 0 ] * (w * 25)
5.times{|k|
r[((x-1)%5) * 5 * w + k * w + z] = 1
r[((x+1)%5) * 5 * w + k * w + ((z-1) % w)] = 1
}
r[x * 5 * w + y * w + z] = 1
r
}
inv = BinMatrix.new(state_equations).inverse
File.open("#{w}_inverted.mat",'wb') do|out|
out.puts(inv.to_s)
end
end
def untheta
unless instance_variable_defined?(:@theta_inv)
precompute_untheta(@w) unless File.exists?("#{@w}_inverted.mat")
@theta_inv = BinMatrix.new(File.open("#{@w}_inverted.mat", "rb", &:read).lines.map{|l| l.chomp.split.map(&:to_i) })
end
# flatten and map to obtain a column matrix representing the current state, B'
# as_state(w) of BinMatrix returns a 3-dimensional state matrix from a BinMatrix.
@state = (@theta_inv * BinMatrix.new(@state.flatten.map{|e|[e]})).as_state(64)
end
\( \rho^{-1} \): Simplier than it looks
The \(\rho\) step essentially loops 24 times, and moves bits within each lane, iterating over each lane exactly once (except for \((0, 0)\), for which no rotation is performed). We checked it by inspecting \((x, y)\) values as iterations advance.
To inverse this step, we simply have to rotate the bits back, we can keep the same iteration order (same order of the lanes to rotate).
- For \(t\) from
0to23- for all \(z\) such that \(0 \leq z <w\), let $$ A[x, y, (z – (t +1)(t + 2)/2)\bmod w] = A’[x, y, z]$$
- let \((x, y) = (y, (2x + 3y)\bmod 5)\)
\( \pi^{-1} \): Inverse transposition
Also a very simple step to inverse. \(\pi\) essentially performs \(A’[x, y, z] = A[(x+3y)\bmod 5, x, z]\) for every \(0 \leq x < 5\), \(0 \leq y < 5\), \(0 \leq z < w\).
This is the algorithm for \(\pi^{-1}\):
- For all \(0 \leq x < 5\), \(0 \leq y < 5\), \(0 \leq z < w\):
- Set \(A[(x+3y)\bmod 5, x, z] = A’[x, y, z]\)
\( \chi^{-1} \): Non-linearity
The \(\chi\) operation is the only non-linear one (non-linear because it includes logical and & operations, which are analog to multiplications).
If we look closely, we notice that the step applies the non-linear function on 5-bit parts, that is, for every \((y, z)\), \(0 \leq y < 5\), \(0 \leq z < w\), the bits at \((x, y, z)\) for every possible value of \(x\) (from 0 to 4) are inputs and outputs of the function.
To inverse it, my approach was to:
- Generate a truth-table of the function, by calculating the nonlinear function image of every value from
00000to11111. - Check if the function is invertible (that it’s a bijection).
- Create a table that maps outputs of the function to inputs.
- Use it to invert the result of \(\chi\) efficiently, that is, apply the inverse function on 5-bit inputs.
def precompute_unchi
# The nonlinear function: A'(x) = A(x) ^ ((!A(x+1)) & A(x+2))
truth_table = (2**5).times.map{|val|
a4, a3, a2, a1, a0 = val >> 4, (val >> 3) & 1, (val >> 2) & 1, (val >> 1) & 1, val & 1;
n4 = a4 ^ ((a3^1) & a2)
n3 = a3 ^ ((a2^1) & a1)
n2 = a2 ^ ((a1^1) & a0)
n1 = a1 ^ ((a0^1) & a4)
n0 = a0 ^ ((a4^1) & a3)
(n4 << 4) | (n3 << 3) | (n2 << 2) | (n1 << 1) | n0
}
# the inverse of the truth table
(2**5).times.map{|val|
truth_table.index val
}
end
def unchi
truth_tbl = precompute_unchi
new_state = clone_state
5.times do|y|
@w.times do|z|
table_line = (@state[0][y][z] << 4) | (@state[1][y][z] << 3) | (@state[2][y][z] << 2) | (@state[3][y][z] << 1) | @state[4][y][z]
inv_num = truth_tbl[table_line]
new_state[0][y][z] = inv_num >> 4
new_state[1][y][z] = (inv_num >> 3) & 1
new_state[2][y][z] = (inv_num >> 2) & 1
new_state[3][y][z] = (inv_num >> 1) & 1
new_state[4][y][z] = inv_num & 1
end
end
@state = new_state
end
\( \iota^{-1} \): Xor again and it’ll be done
This step is very easy to inverse, all it does is to xor some values in the state with some round constants.
To invert it, we just have to perform it again (the same round constants will be generated, and xors will cancel out).
def uniota(ir)
iota(ir)
end
\(Keccak-p^{-1}\): Just perform the inverse operations in reverse order
As a reminder, the \(Keccak-p\) function performs the following steps:
- Convert the input string
S(of lengthb) to a 3-dimensional state arrayA(of the shape \( 5 \times 5 \times w \)) . Bits are just rearranged. - Runs the following operations \(n_r\) times (\(i_r\) being the round index,
0,1…).- \( A’ = \iota ( \chi ( \pi ( \rho ( \theta ( A ) ) ) ), i_r ) \)
- \( A’ \) becomes the new state
- Convert the state to a string
S(of lengthb), bits are just rearranged, as in the first step.
Inversing it becomes trivial, the following are the steps:
- Convert the input string
S(of lengthb) to a 3-dimensional state arrayA'(of the shape \( 5 \times 5 \times w \)) . Bits are just rearranged. - Runs the following operations \(n_r\) times (\(i_r\) being the round index), for \(i_r\) from \(n_r\) to
0.- \( A = \theta^{-1}(\rho^{-1}(\pi^{-1}(\chi^{-1}(\iota^{-1}(A’, i_r))))) \)
- \( A \) becomes the new state
- Convert the state to a string
S(of lengthb), bits are just rearranged, as in the first step.
def unkeccak_rho(s, nr)
state_from_bitarray s;
l = Math.log(@w, 2).to_i
(12+2*l-1).downto(12+2*l-nr) do|ir|
uniota(ir)
unchi
unpi
unrho
untheta
end
bitarray_from_state
end
That’s it! we’ve successfully inverted the permutation at the core of the Keccak algorithm.
Example testing
# generate a vector of 1600 random bits
msg = 1600.times.map{ [0, 1].sample }
output = keccak_f(msg)
inverse = unkeccak_f(output)
if inverse == msg
puts "[+] Inverting Keccak-f was successful"
else
puts "[-] Didn't retrieve the original message after inverting keccak-f"
end
You can find the full program here.
The inverse of the \(1600\times 1600\) matrix can be found here. (It’ll take a few minutes to compute it on the first run)
Implications
The permutation function is known to be invertible, it’s a permutation function after all, this doesn’t make the whole hash function vulnerable. However, this property can lead to unwanted consequences, depending on the attack model we consider.
Looking back at the sponge construction, at least \(c\) bytes of the internal state will not be returned as output from the function. This property makes it one-way, if an attacker can recover the full state (\(5\times 5\times w\) matrix), he will be able to inverse the keccak permutation function, and if the input message consists of only one block, it’s possible to recover the initial vector of (\((0^r \oplus P) || 0^c\)), which includes the plaintext message \(P\).